软件分析课程笔记

本文是基于南京大学《软件分析》课程的个人笔记¹²，仅供自用

一、程序的表示¶

1 概述¶

Definition: 静态分析（Static Analysis） 是指在实际运行程序 \(P\) 之前，通过分析静态程序 \(P\) 本身来推测程序的行为，并判断程序是否满足某些特定的性质（Property） \(Q\)

Rice定理（Rice Theorem）：对于使用递归可枚举（Recursively Enumerable）的语言描述的程序，其任何非平凡（Non-trivial）的性质都是无法完美确定的。

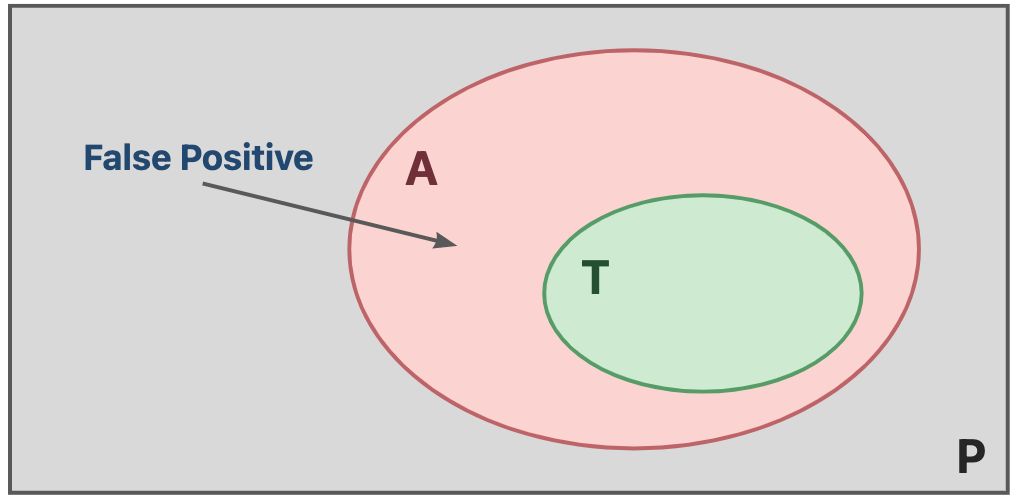
由上可知不存在完美的程序分析，要么满足完全性（Soundness），要么满足正确性（Completeness）。Sound 的静态分析保证了完全性，妥协了正确性，会过近似（Overapproximate）程序的行为，因此会出现假阳性（False Positive）的现象，即误报问题。现实世界中，Sound的静态分析居多，因为误报可以被暴力排查，而Complete的静态分析存在漏报，很难排查。

Static Analysis: ensure (or get close to) soundness, while making good trade-offs between analysis precision and analysis speed.

两个词概括静态分析：抽象，过近似

过近似上文已经提到过了，这里说明一下抽象，即将具体值转化为符号值。例如将如下表左侧具体值转化为右侧抽象符号

具体值	抽象值
v = 1000	+
v = -1	-
v = 0	0
v = x ? 1 : -1	（丅）unknown
v = w / 0	（丄）undefined

接下来就可以设计转移方程（ Transfer functions），即在抽象值上的操作

![note_static_analysis-002.png]

再看一个例子，体会一下 Sound 的，过近似的分析原则：

x = 1;
if input then
    y = 10;
else
    y = -1;
z = x + y;

我们会发现，在进入 2-5 行的条件语句的时候， \(y\) 的值可能为 \(10\) ，也可能为 \(-1\) ，于是，我们最终会认为y的抽象值为 \(\top\) ，最终 \(z\) 的抽象值也就为 \(\top\) ，这样，我们的分析就是尽可能全面的，虽然它并不精确。

2 中间表示¶

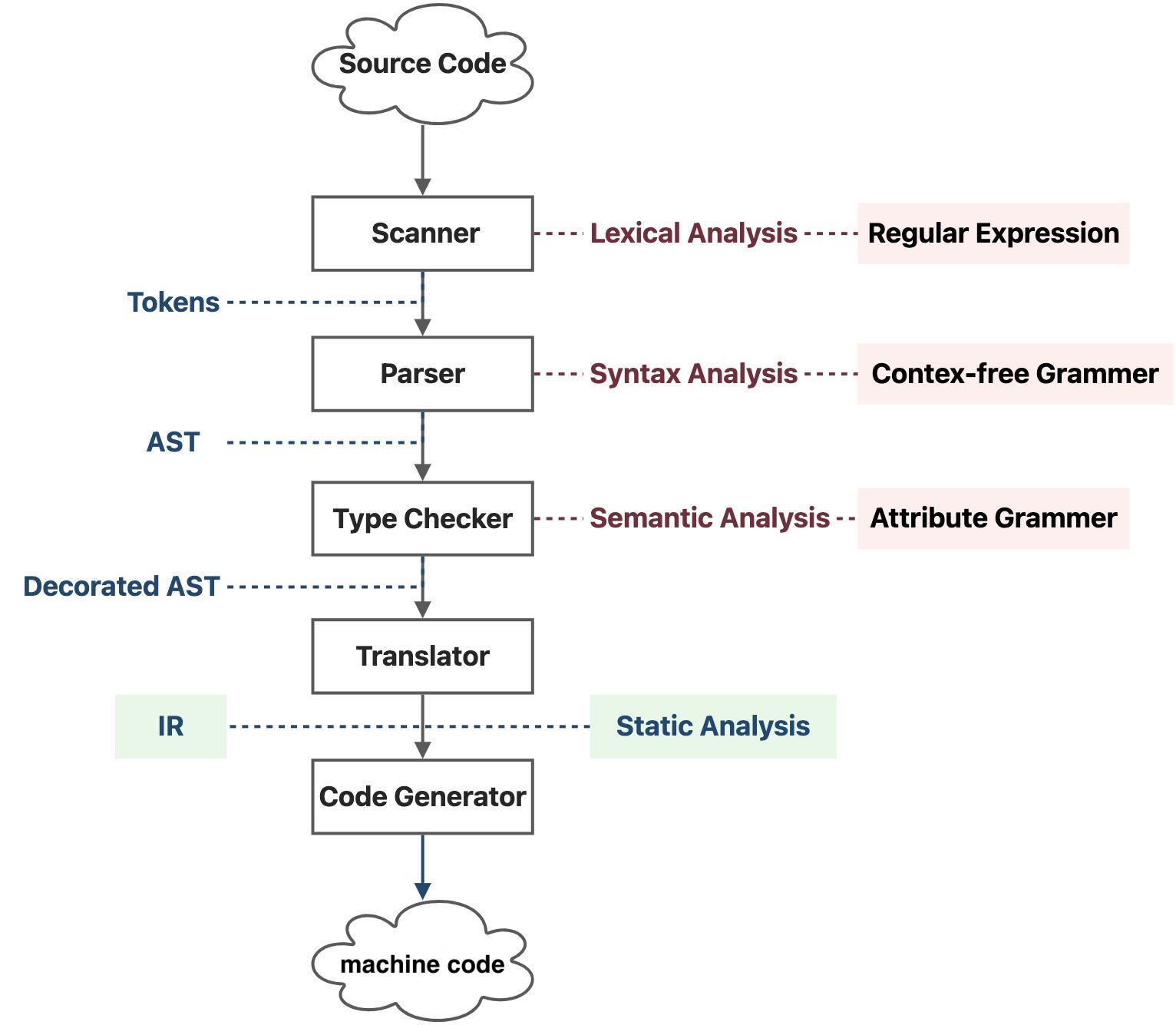
编译器和静态分析器¶

静态分析一般发生在 IR 层

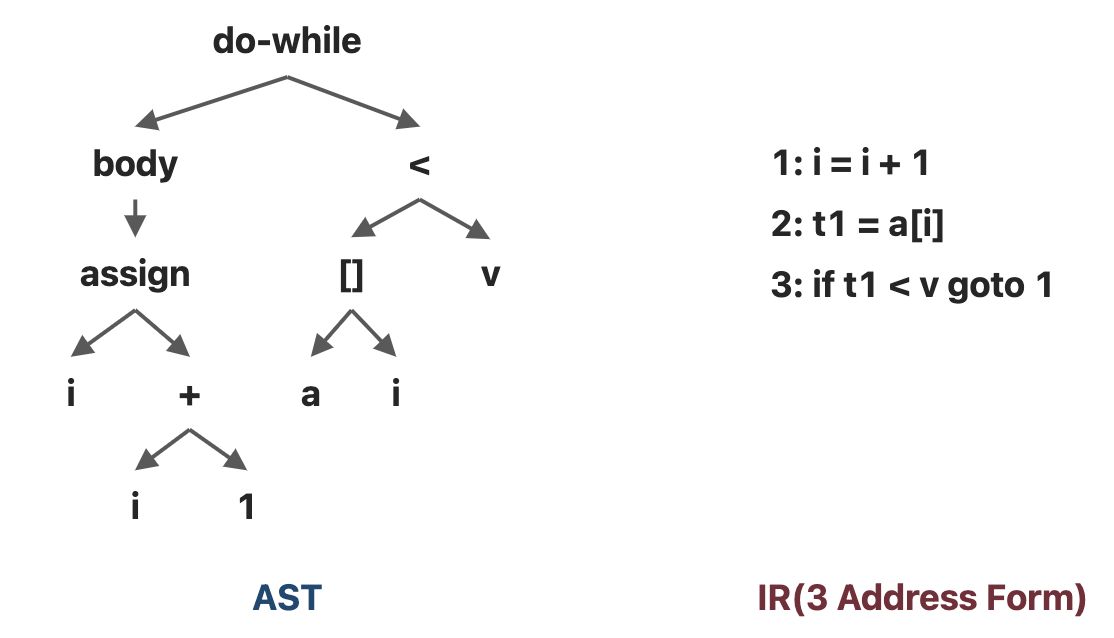
考虑下面一小段代码：

do i = i + 1; while (a[i] < v);

AST和三地址码 IR 如下

AST	IR
层次更高，和语法结构更接近	低层次，和机器代码相接近
通常是依赖于具体的语言类的	通常和具体的语言无关，主要和运行语言的机器（物理机或虚拟机）有关
适合快速的类型检查	简单通用
缺少和程序控制流相关的信息	包含程序的控制流信息
	通常作为静态分析的基础

Definition: 我们将形如 \(f(a_1, a_2, ..., a_n)\) 的指令称为 \(n\) 地址码（N-Address Code），其中，每一个 \(a_i\) 是一个地址，既可以通过 \(a_i\) 传入数据，也可以通过 \(a_i\) 传出数据， \(f\) 是从地址到语句的一个映射，其返回值是某个语句 \(s\) ， \(s\) 中最多包含输入的 \(n\) 个地址。这里，我们定义某编程语言 \(L\) 的语句 \(s\) 是 \(L\) 的操作符、关键字和地址的组合。
3地址码（3-Address Code，3AC），每条 3AC 至多有三个地址。而一个「地址」可以是：名称 Name:，例如a, b；常量 Constant，例如 3；编译器生成的临时变量 Compiler-generated Temporary，例如 t1，t2

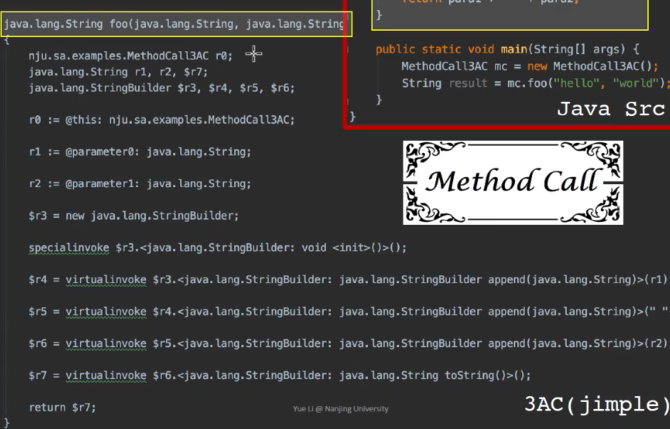
以Soot与它的 IR 语言 Jimple为例

package ecool.examples;
public class MethodCall3AC{
    String foo(String para1, String para2) {
        return para1 + " " + para2;
    }

    public static void main(String[] args){
        MethodCall3AC mc = new MethodCall3AC();
        String result = mc.foo("hello", "world");
    }
}

静态单赋值（Static Single Assignment，SSA）是另一种IR的形式，它和3AC的区别是，在每次赋值的时候都会创建一个新的变量，也就是说，在SSA中，每个变量（包括原始变量和新创建的变量）都只有唯一的一次定义。

控制流分析¶

基块

控制流分析（Control Flow Analysis, CFA）通常是指构建控制流图（Control Flow Graph，CFG）的过程。CFG是我们进行静态分析的基础，控制流图中的结点可以是一个指令，也可以是一个基块（Basic Block）。

简单来讲，基块就是满足两点的最长的指令序列：第一，程序的控制流只能从首指令进入；第二，程序的控制流只能从尾指令流出。构建基块的算法如下

找到所有的leaders：程序的入口为leader；跳转的target为leader；跳转语句的后一条语句为leader
以leader为分割点取最大集

控制流图 CFG

构建算法如下

对所有最后一条语句不是跳转的basic block与其相邻的basic block相连
对有最后一条语句是有条件跳转的basic block，与其相邻的basic block和其跳转的basic block相连
对于最后一条语句是无条件跳转的basic block，直接将其于跳转的basic block相连

此外，对于控制流图来说还有两个概念Entry 和 Exit

Entry即程序的入口，通常是第一个语句，一般来说只有一个
Exit则是程序的出口，通常是return之类的语句，可能会有多个

二、数据流分析与应用¶

3 数据流分析——应用¶

数据流分析初步¶

Definition: 数据流分析（Data Flow Analysis, DFA）是指分析“数据在程序中是怎样流动的”。具体来讲，其分析的对象是基于抽象（概述中提到）的应用特定型数据（Application-Specific Data）；分析的行为是数据的“流动（Flow）”，分析的方式是安全近似（Safe-Approximation），即根据安全性需求选择过近似（Over-Approximation）还是欠近似（Under-Approximation）；分析的基础是控制流图（Control Flow Graph, CFG），CFG是程序 \(P\) 的表示方法；

数据流动的场景有两个：

Transfer function：在CFG的点（Node）内流动，即Basic block内部的数据流；
Control-flow handling：在CFG的边（Edge）上流动，即由基块间控制流触发的数据流。
输入输出状态

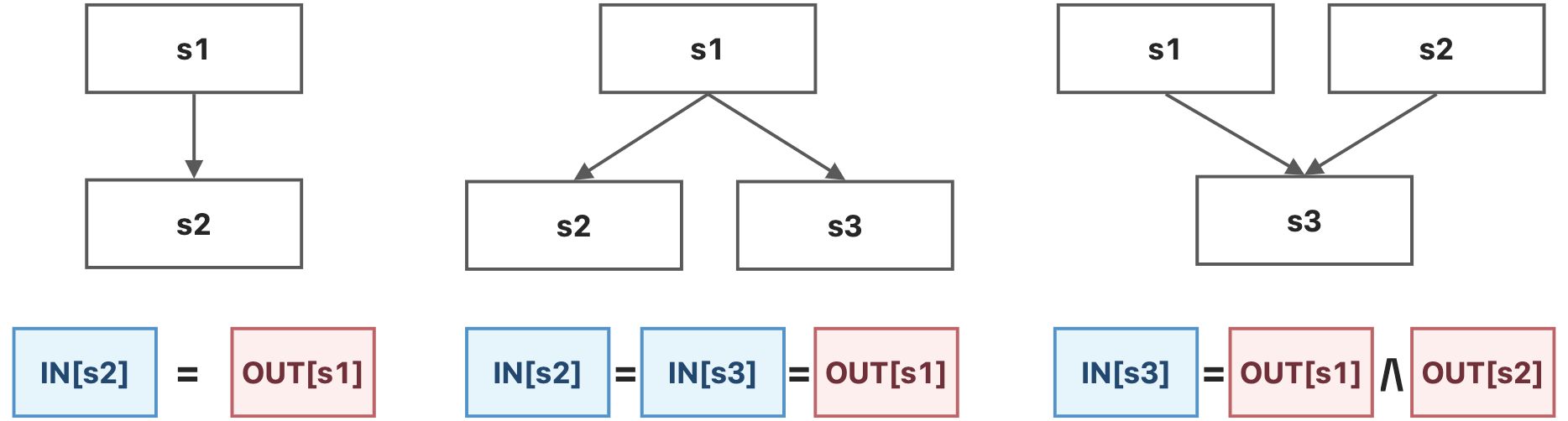
下图中是常见的几种程序上下文状态，在每个具体的数据流分析中，我们最终会为每一个程序点关联一个数据流值，这个数据流值表征了在这个程序点能够观察到的所有可能的程序状态

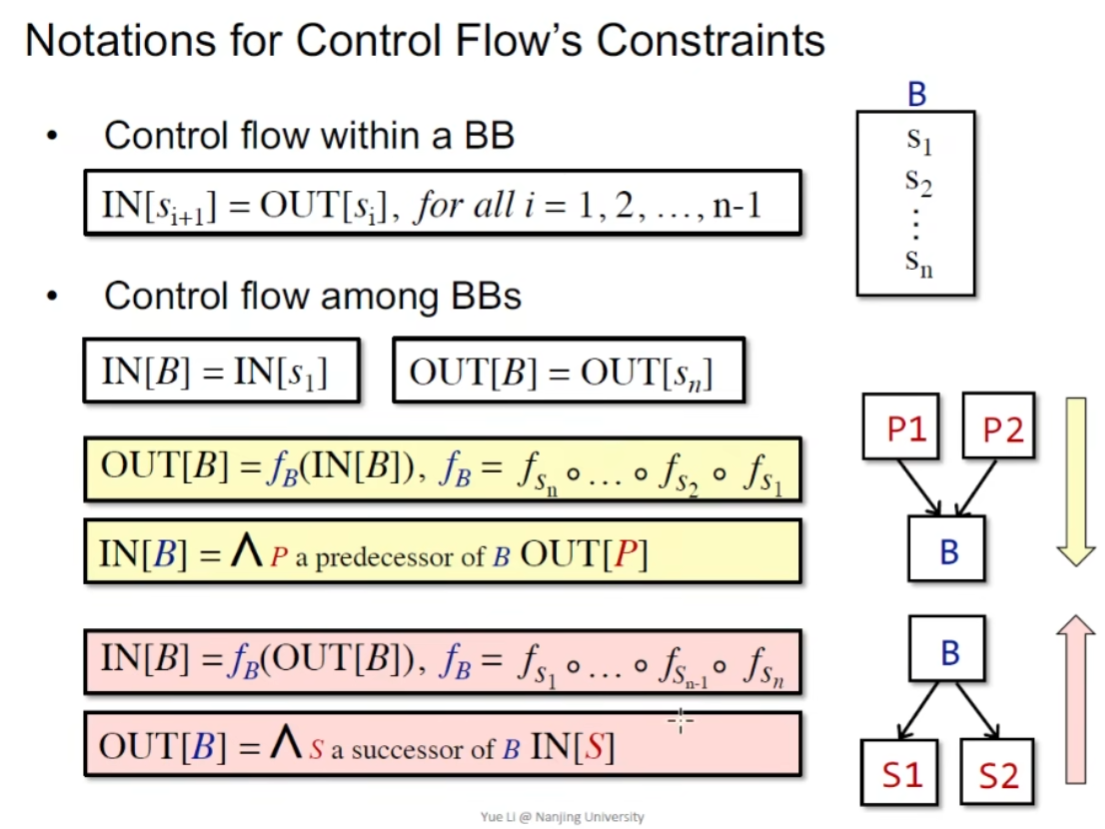
现在，我们能够定义，数据流分析就是要寻找一种解决方案（即 \(f_{pp}->D\) ），对于程序 \(P\) 中的所有语句 \(s\) ，这种解决方案能够满足 \(IN[s]\) 和 \(OUT[s]\) 所需要满足的 安全近似导向型约束（Safe-Approximation-Oriented Constraints, SAOC），SAOC主要有两种：

基于语句语意（Sematics of Statements）的约束，即由状态转移方程产生的约束；
基于控制流（Flow of Control）的约束，即上述输入输出状态所产生的约束。

定义可达性分析¶

当前阶段假设程序中不存在method call
当前阶段假设程序中不存在aliaes，别名

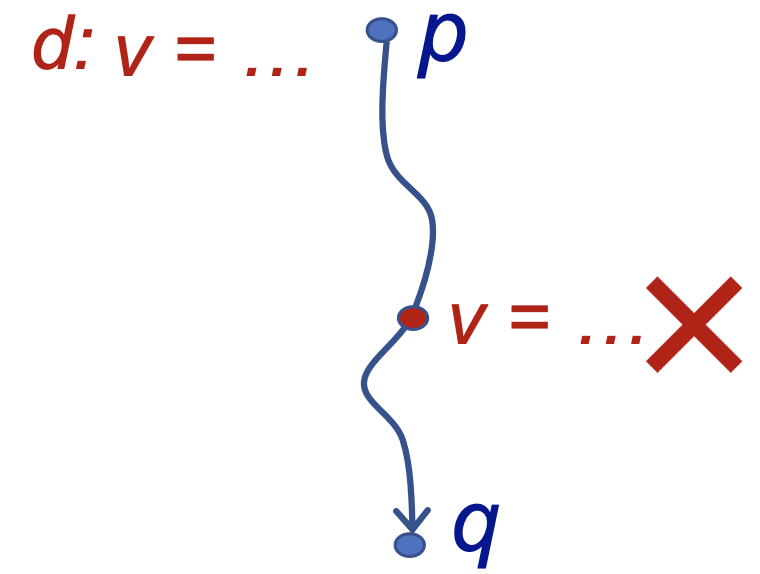
Definition: 我们称在程序点 \(p\) 处的一个定义 \(d\) 到达（Reach） 了程序点 \(q\) ，如果存在一条从 \(p\) 到 \(q\) 的“路径”（控制流），在这条路径上，定义 \(d\) 未被覆盖（Kill）。称分析每个程序点处能够到达的定义的过程为 定义可达性分析（Reaching Definition Analysis）

定义可达性分析用来检测程序中是否存在未定义的变量。例如，我们在程序入口为各个变量引入一个伪定义（dummy definition）。如果程序中存在某个使用变量 \(v\) 的程序点 \(p\) ，且 \(v\) 的伪定义能够到达程序点 \(p\) ，那么我们就可以分析出变量 \(v\) 可能在定义之前被使用，也就是可能程序存在变量未定义的错误（实际程序执行的时候，只有唯一的一条控制流会被真实的执行，而这条控制流并不一定刚好是我们用于得到定义可达结论的那一条）。同时，当执行到程序出口时，该变量定值依然为dummy，则可以认为该变量未被定义。

从上述的定义中，能够看出这是一个可能性分析（May Analysis），采用的是过近似（Over-Approximation）的原则，且属于前向（forward）分析

在看这个算法之前，我们定义语句 D: v = x op y 生成了关于变量 v 的一个新定义 D ，并且覆盖了程序中其他地方对于变量 v 的定义，不过并不会影响后续其他的定义再来覆盖这里的定义。赋值语句只是定义的一种形式而已，定义也可以有别的形式，比如说引用参数。

我们假设程序 \(P\) 中所有的定义为 \(D = \{d_1, d_2, ..., d_n\}\) ，于是，我们可以用 \(D\) 的子集（即定义域中的元素）来表示每个程序点处，能够到达该点的定义的集合，即该程序点处的数据流值。其实也就是确定 \(f_{PP \to D}\) ，为每一个程序点关联一个数据流值。

在具体的实现过程中，因为全集 \(D\) 是固定的，且我们记 \(|D| = n\) ，所以我们可以采用 \(n\) 位的位向量（Bit Vector）来表示 \(D\) 的所有子集，也就是我们所有可能的抽象数据状态。其中位向量从左往右的第 \(i\) 位表示定义 \(d_i\) 是否可达，具体地，第 \(i\) 位为 \(0\) 表示 \(d_i\) 不可达，为 \(1\) 则可达。

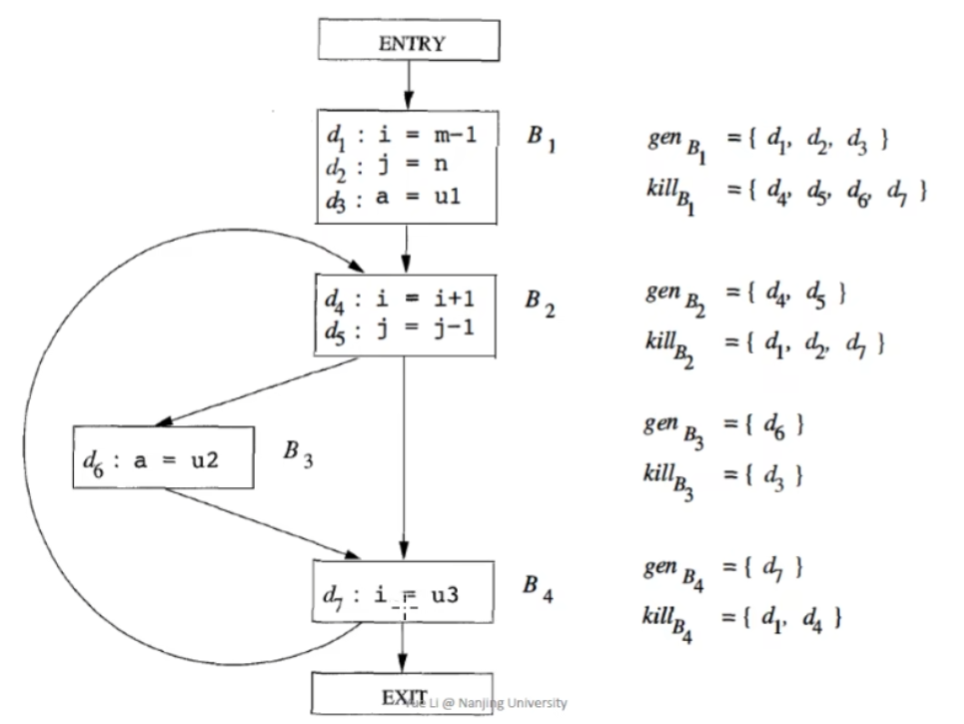
我们以基块为粒度考虑问题，一个基块中可能有许多具有定义功能的语句，基块B所产生的新的定义记为集合 \(gen_B\) ，这些定义语句会覆盖其他地方的别的对于相关变量的定义，基块B所覆盖掉的定义记为集合 \(kill_B\)。下面用一个例子进行说明。

对于一个静态的程序来说， \(kill_B\) 和 \(gen_B\) 都是固定不变的。在此基础上，我们可以得到一个基块 \(B\) 的转移方程为：

\[ OUT[B] = gen_B \cup (IN[B] - kill_B) \]

考虑 控制流的约束 ，因为我们采用的是过近似方式，因此一个定义达到某个程序点，只需要有至少一条路径能够到达这个点即可。因此，我们定义交汇操作符为集合的并操作，即 \(\wedge = \cup\) ，则控制流约束为：

\[ IN[B] = \bigcup_{P \in pre(B)} OUT[P] \]

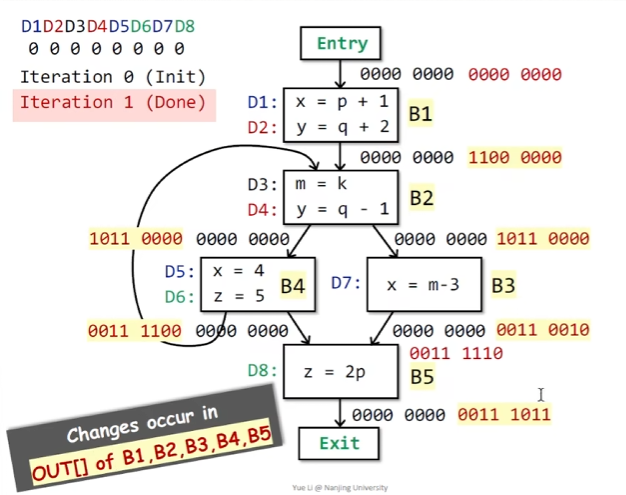
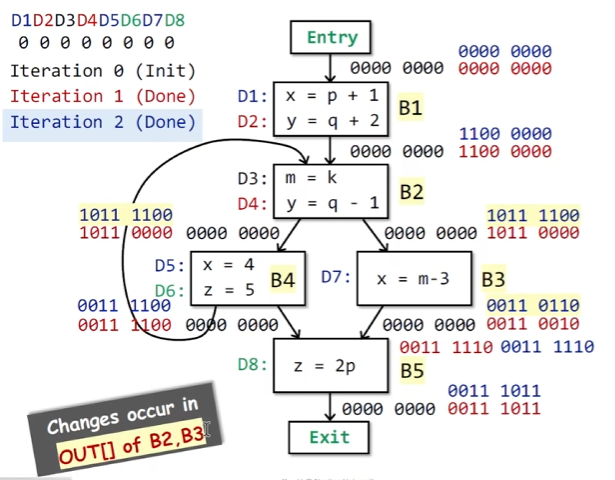
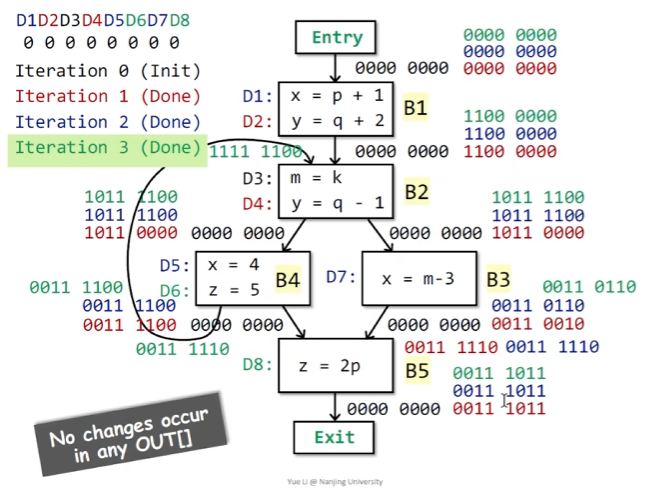
算法具体内容如下

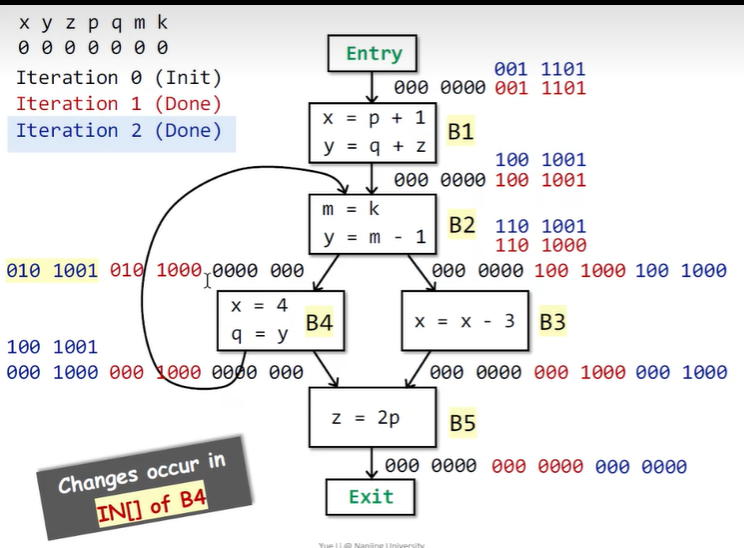
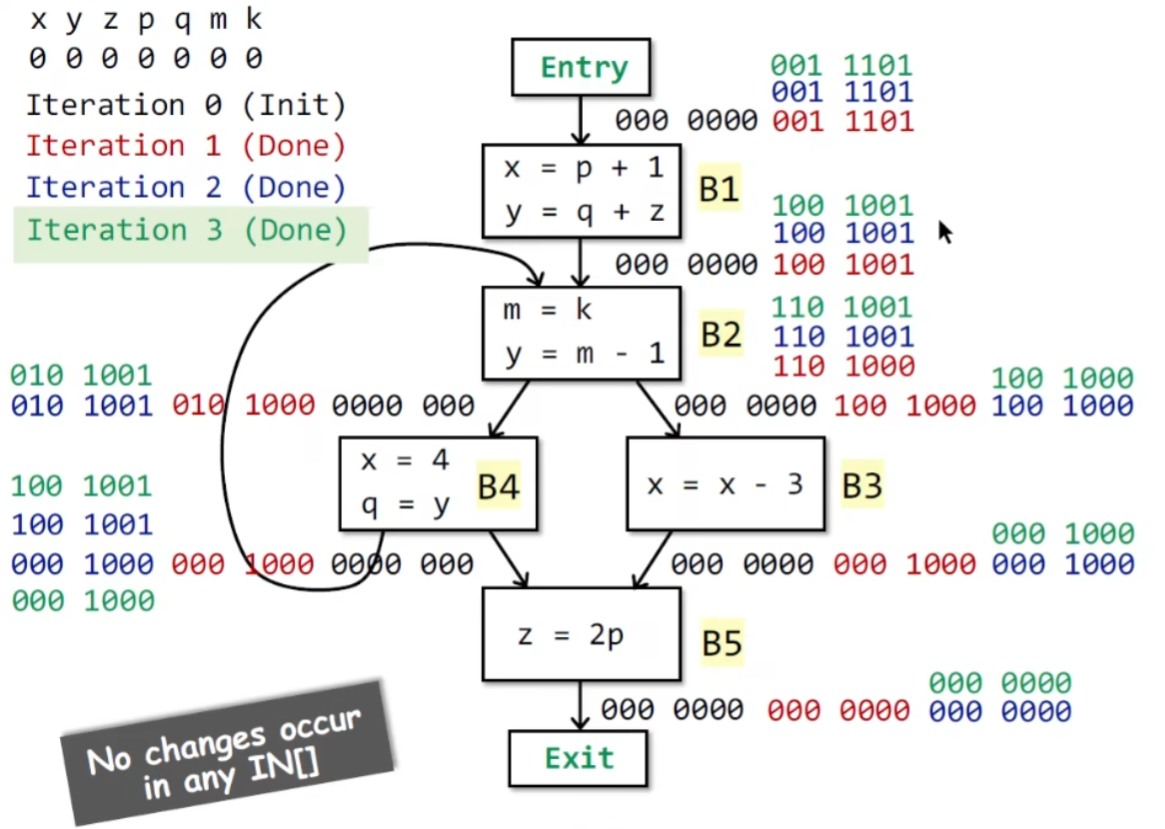
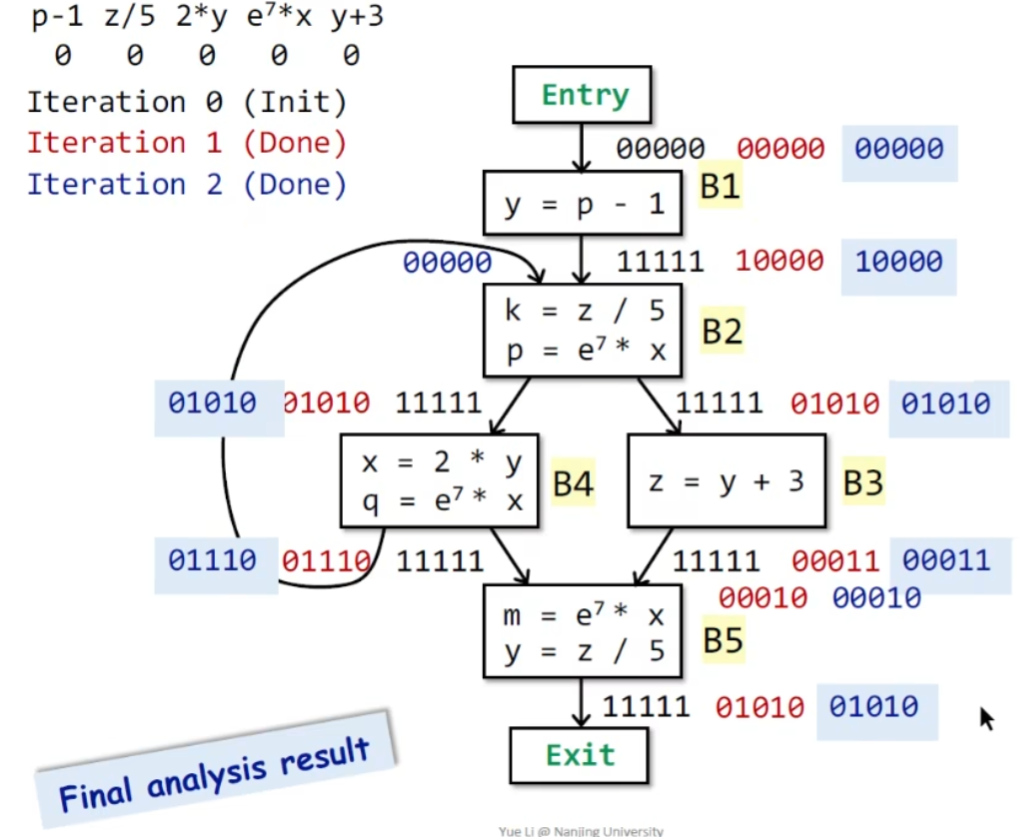
用一个例子来说明上述的算法

当没有BB的状态变化时，算法结束，这时我们就能够看到这个算法表示的真正含义，举例来说，在B3的OUT结果为00110110，即我们能够观察到D3，D4，D6，D7的定义能够到达该点。

为什么这个算法能够停止

\(gen_B\) 和 \(kill_B\) 是不变的，因为程序P本身是不改变的（至少我们现在的分析场景下是这样的）；

当更多的定义从控制流流入 \(IN[B]\) （也就是当别处的定义到达B的时候），这里流入的更多的定义：要么被 \(kill_B\) 给覆盖了；要么幸存了下来，流入了 \(OUT[B]\) ，记为 \(survivor_B = IN[B] - kill_B\) 。也就是说，当一个定义d被加入 \(OUT[B]\) 集合的时候，无论是通过 \(gen_B\) 还是 \(survivor_B\) ，它会永远的留在 \(OUT[B]\) 中；因为这一轮的幸存者在下一轮依然是幸存者（ \(kill_B\) 是固定的）。因此，集合 \(OUT[B]\) 是不会收缩的，也就是说 \(OUT[B]\) 要么变大，要么不变。而定义的总集合 \(D\) 是固定的，而 \(OUT[B] \subseteq D\) ，因此最终一定会有一个所有的 \(OUT[B]\) 都不变的状态。

更具体的，当 \(OUT\) 不变的时候，由于 \(IN[B] = \bigcup_{P\in pre(B)} OUT[P]\) ，\(IN\) 也就不变了，而 \(IN\) 不变的话，由于 \(OUT[B] = gen_B\cup (IN[B] - kill_B)\) ，则 \(OUT\) 也就不变了。此时，我们称这个迭代的算法到达了一个“不动点（Fixed Point）”，这也和算法的单调性（Monotonicity）有关。

活跃变量分析¶

Definition: 在程序点 \(p\) 处，某个变量 \(v\) 的变量值（Variable Value）可能在之后的某条控制流中被用到，我们就称变量 \(v\) 是程序点 \(p\) 处的 活变量（Live Variable） ，否则，我们就称变量 \(v\) 为程序点 \(p\) 处的 死变量（Dead Variable） 。分析在各个程序点处所有的变量是死是活的分析，称为 活跃变量分析（Live Variable Analysis） 。

即，程序点 \(p\) 处的变量 \(v\) 是活变量，当且仅当在 CFG 中存在某条从 \(p\) 开始的路径，在这条路径上变量 \(v\) 被使用了，并且在 \(v\) 被使用之前， \(v\) 未被重定义。

活跃变量分析可以应用在寄存器分配（Register Allocation）中，可以作为编译器优化的参考信息。比如说，如果在某个程序点处，所有的寄存器都被占满了，而我们又需要用一个新的寄存器，那么我们就要从已经占满的这些寄存器中选择一个去覆盖它的旧值，我们应该更青睐于去覆盖那些储存死变量的寄存器。

综上，活跃变量分析适合用逆向分析（backward）的方式来进行。

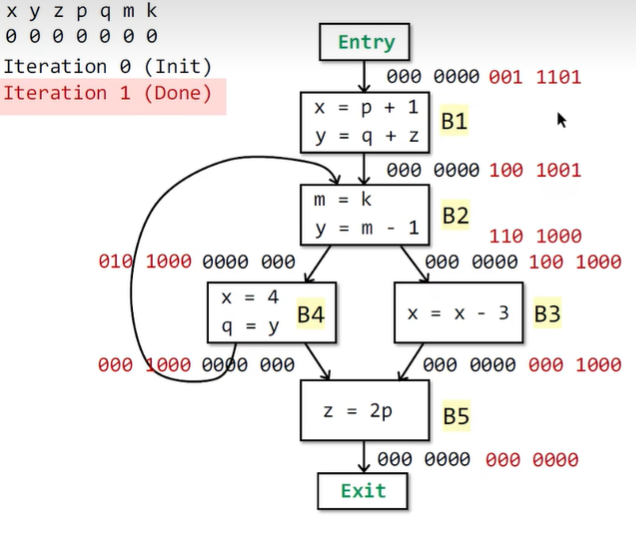
算法具体内容如下

用一个例子来说明上面的算法

结果输出后，举例来说，\(IN[B2]\) 的值为1001001，即此时x，p，k变量还是live的。

可用表达式分析¶

Definition：我们称一个表达式（Expression）x op y在程序点 \(p\) 处是 可用的（Avaliable） ，如果：所有的从程序入口到程序点 \(p\) 的路径都必须经过 x op y 表达式的评估（Evaluation），并且在最后一次 x op y 的评估之后，没有 \(x\) 或者 \(y\) 的重定义（Redefinition）。对于程序中每个程序点处的可用表达式的分析，我们称之为 可用表达式分析（Avaliable Expression Analysis）

在这个问题中，考虑程序中所有表达式的集合，即 \(E = \{e_1, e_2, ..., e_n\}\) ，其中 \(e_i\) 是程序中的表达式。那么，每个程序点处的抽象程序状态，也就是数据流值，则为 \(E\) 的一个子集，整个分析的定义域 \(D = 2^E\) 。之后我们只需要建立 \(f_{PP\to D}\) 即可

这里说一个表达式是可用的，指的是这个表达是的值肯定已经被计算过了，可以直接复用之前的结果，没必要再算一遍，也就是说，这个表达式 不需要忙碌于计算 。我们考虑一个简单的场景。

if a - b > c then
    c = a - b;

d = a - b;
if d > c then
  c = d

上面两个例子功能性上是等价的，但是在 Example 01 中， a - b 被重复计算了两次，而 Example 02 中， a - b 只被计算了一次，因此 Example 02 的效率是更高的。在 Example 01 的第2行， a - b 就是一个可用表达式，在之前肯定已经被计算过，因此我么可以对程序进行优化，通过一个变量或者是寄存器储存之前的计算结果，从而在之后不需要进行重复的计算。

可用表达式的相关信息还可以被用来检测全局的公共子表达式（Global Common Subexpression）。

从定义中不难看出，可用表达式分析是一种必然性分析。因为在上述表达式优化的应用场景中，我们可以不优化每一个表达式，但不可以优化错误（也就是说一旦决定优化某个表达式，这个表达式就必须必然是可用表达式）。

算法的具体内容如下：

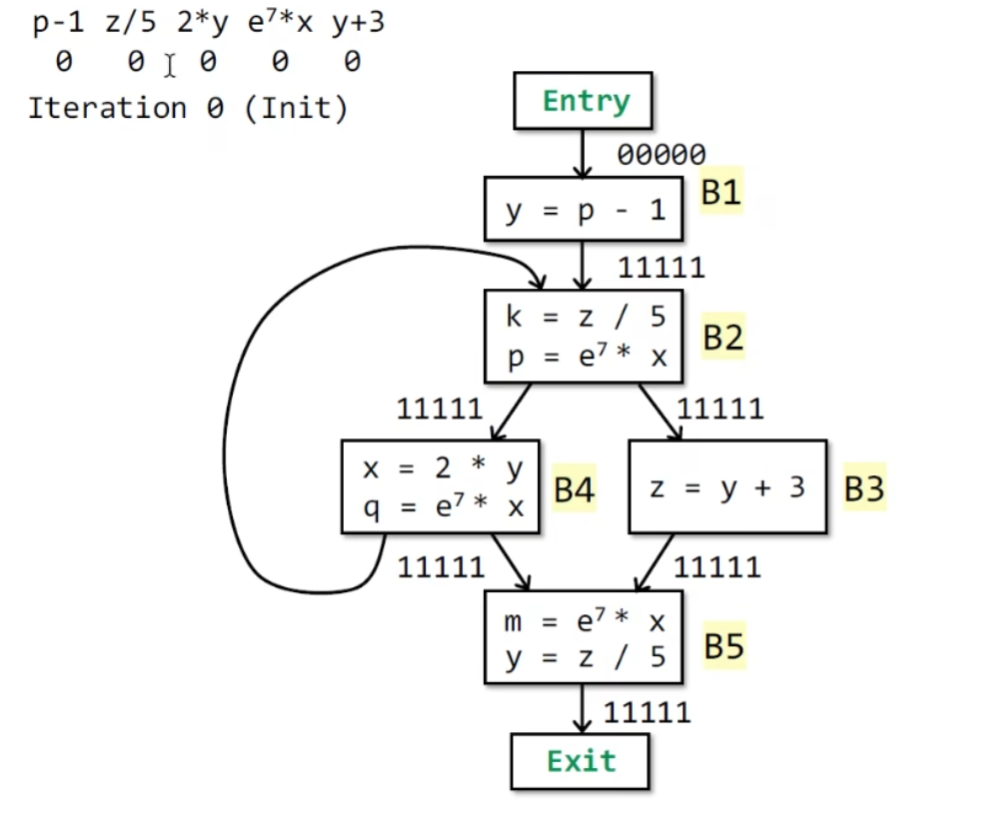
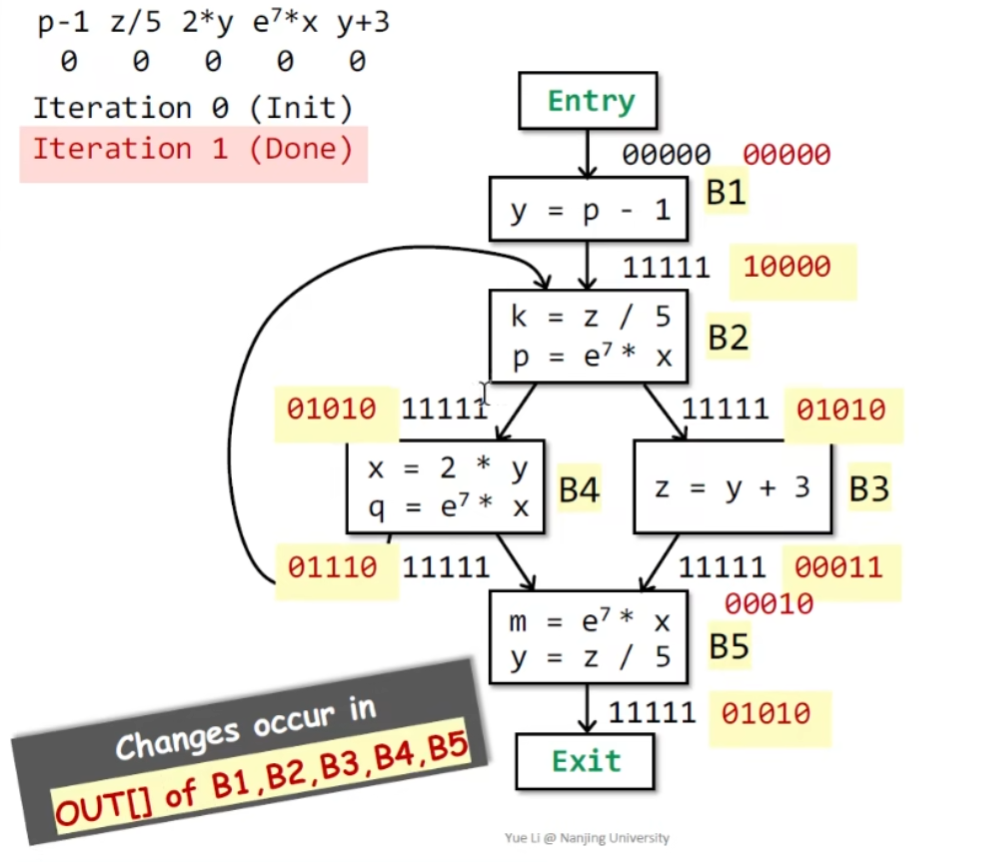
下面用一个例子说明这个算法：

总结¶

	定义可达性分析	活跃变量分析	可用表达式分析
定义域	定义集的幂集	变量集的幂集	表达式集的幂集
方向	正向分析	逆向分析	正向分析
估计	过近似	过近似	欠近似
边界	\(OUT[ENTRY]=\emptyset\)	\(IN[EXIT]=\emptyset\)	\(OUT[ENTRY]=\emptyset\)
初始化	\(OUT[B] = \emptyset\)	\(IN[B]=\emptyset\)	\(OUT[B] = U\)
状态转移	\(OUT[B] = gen_B \cup (IN[B] - kill_B)\)	\(IN[B] = use_B \cup (OUT[B] - def_B)\)	\(OUT[B] = gen_B \cup (IN[B] - kill_B)\)
交汇	\(IN[B] = \bigcup\limits_{P \in pre(B)} OUT[P]\)	\(OUT[B] = \bigcup\limits_{S \in suc(B)} IN[S]\)	\(IN[B] = \bigcap\limits_{P \in pre(B)} OUT[P]\)

数据流分析的基本过程

问题描述：定义要研究的问题，从而确定分析顺序（正向还是逆向）和估计方式（过近似还是欠近似）；
数据抽象：确定抽象数据状态集（也就是数据流值集），从而确定定义域；
约束分析：考虑语意约束，确定状态转移方程；考虑控制流约束，确定交汇操作符的含义；
算法设计：根据上述分析设计算法，我们目前只学了迭代算法，还可以有其他的算法设计；
算法分析：分析算法的正确性和复杂度。

4 数据流分析——基础¶

重新审视迭代算法¶

下面我们从另一个视角来审视一下迭代算法。

给定一个具有 k 个结点的程序流程图CFG，对于CFG中的每个结点 \(n\) ，迭代算法的每一次迭代都会更新 \(OUT[n]\) ；
设数据流分析的定义域为 \(V\) ，我们可以定义一个 \(k\) 元组（k-tuple）来表示每次迭代后的分析值：

\[ (OUT[n_1], OUT[n_2], ..., OUT[n_k]) \in V \times V \times ... \times V = V^k \]

每次迭代可以视为将 \(V^k\) 中的某个值映射为 \(V^k\) 中的另一个值，通过状态转移方程和控制流约束式，这个过程可以抽象为一个函数 \(F_{V^k \to V^k}\) ；
然后这个算法会输出一系列的k元组，直到某两个连续输出的k元组完全相同的时候算法终止。

于是，算法的过程可以表示为：

初始化	\((\bot, \bot, ..., \bot) = X_0\)
第1次迭代	\((v_1^1, v_2^1, ..., v_k^1) = X_1 = F(X_0)\)
第2次迭代	\((v_1^2, v_2^2, ..., v_k^2) = X_2 = F(X_1)\)
......	......
第i次迭代	\((v_1^i, v_2^i, ..., v_k^i) = X_i = F(X_{i - 1})\)
第i+1次迭代	\((v_1^i, v_2^i, ..., v_k^i) = X_{i + 1} = F(X_i) = X_i\)

其中， \(v_i^j\) 表示第 i 个结点第 j 次迭代后的数据流值。

算法终止的时候，我们发现 \(X_{i + 1} = F(X_i) = X_i\) ，因此 \(X_i\) 是函数 \(F\) 的一个不动点（Fixed Point），故而我们称算法到达了一个不动点。

数学抽象¶

Partial Order 偏序

我们定义偏序集（Poset）为 \((P, \preceq)\) ，其中 \(\preceq\) 为一个二元关系（Binary Relation），这个二元关系在 \(P\) 上定义了 偏序（Partial Ordering） 关系，并且 \(\preceq\) 具有如下性质：

自反性（Reflexivity） ： \(\forall x\in P, x \preceq x\) ；
反对称性（Antisymmetry） ： \(\forall x, y\in P, x \preceq y \wedge y \preceq x \Rightarrow x = y\) ；
传递性（Transitivity） ： \(\forall x, y, z \in P, x \preceq y \wedge y \preceq z \Rightarrow x \preceq z\) 。
格

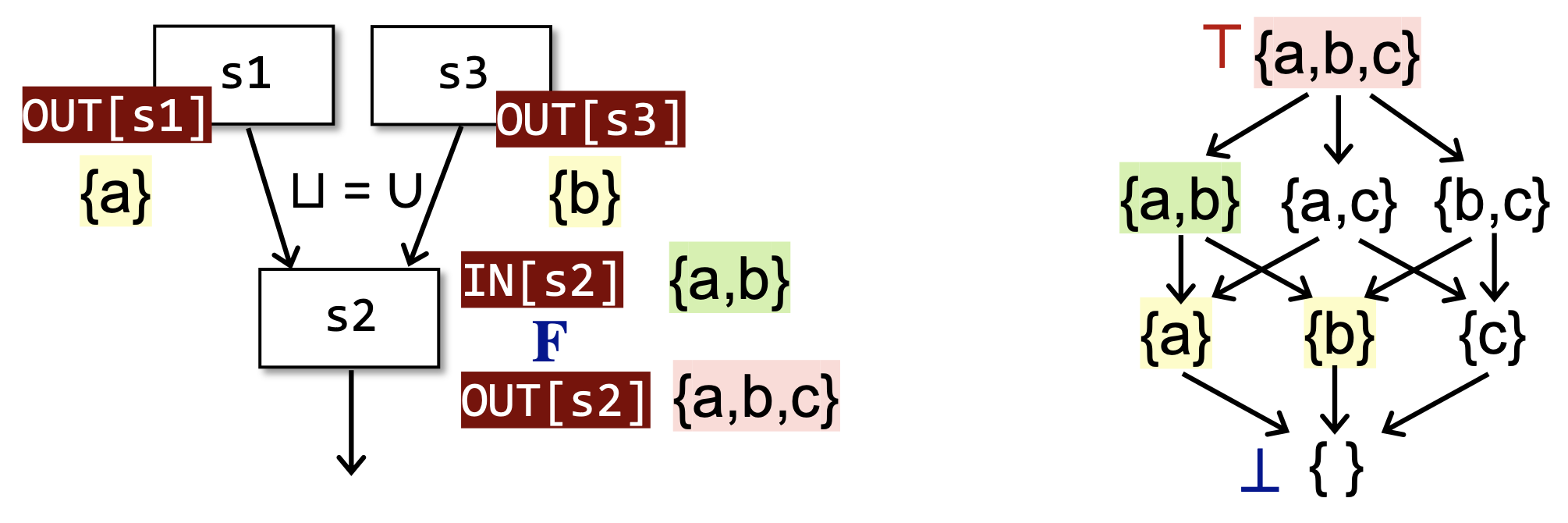
考虑偏序集 \((P, \preceq)\) ，如果 \(\forall a, b\in P\) ， \(a\vee b\) 和 \(a \wedge b\) 都存在，则我们称 \((P, \preceq)\) 为 格（Lattice） 。

简单理解，格是每对元素都存在最小上界和最大下界的偏序集。比如说 \((Z, \le)\) 是格，其中 \(\vee = \max, \wedge = \min\) ； \((2^S, \subseteq)\) 也是格，其中 \(\vee = \cup, \wedge = \cap\) 。

考虑偏序集 \((P, \preceq)\) ，如果 \(\forall S \subseteq P\) ， \(\vee S\) 和 \(\wedge S\) 都存在，则我们称 \((P, \preceq)\) 为 全格（Complete Lattice） 。简单理解，全格的所有子集都有最小上界和最大下界。由于 \((Z, \le)\) ，子集 \(Z_{+}\) 没有最小上界，因此它不是全格；与之不同的， \((2^S, \subseteq)\) 就是一个全格。

每一个全格 \((P, \preceq)\) 都有一个 序最大（Greatest） 的元素 \(\top = \vee P\) 称作 顶部（Top） ，和一个 序最小（Least） 的元素 \(\bot = \wedge P\) 称作 底部（Bottom） 。

每一个有限格（Finite Lattice） \((P, \preceq)\) （ \(P\) 是有限集）都是一个全格。

考虑偏序集 \(L_1 = (P_1, \preceq_1), L_2 = (P_2, \preceq_2), ..., L_n = (P_n, \preceq_n)\) ，其中 \(L_i = (P_i, \preceq_i), i = 1, 2, ..., n\) 的LUB运算为 \(\vee_i\) ，GLB运算为 \(\wedge_i\) ，定义 积格（Product ） 为 \(L^n = (P, \preceq)\) ，满足：

\(P = P_1 \times P_2 \times ...\times P_n\)
\((x_1, x_2, ..., x_n) \preceq (y_1, y_2, ..., y_n) \Leftrightarrow (x_1 \preceq y_1) \wedge (x_2 \preceq y_2) \wedge ... \wedge (x_n \preceq y_n)\)
\((x_1, x_2, ..., x_n) \wedge (y_1, y_2, ..., y_n) = (x_1 \wedge y_1, x_2 \wedge y_2, ..., x_n \wedge y_n)\)
\((x_1, x_2, ..., x_n) \vee (y_1, y_2, ..., y_n) = (x_1 \vee y_1, x_2 \vee y_2, ..., x_n\vee y_n)\)

积格是格。

全格的积格还是全格。

不动点

我们称一个函数 \(f_{L\to L}\) （ \(L\) 是格）是 单调的（Monotonic） ，具有 单调性（Monotonicity） ，如果 \(\forall x, y\in L, x\preceq y \Rightarrow f(x) \preceq f(y)\) 。

考虑一个全格 \((L, \preceq)\) ，如果 \(f_{L\to L}\) 是单调的且 \(L\) 是有限集，那么 序最小的不动点（Least Fixed Point） 可以通过如下的迭代序列找到：

\[ f(\bot), f(f(\bot)), ..., f^{h + 1}(\bot) \]

序最大的不动点（Greatest Fixed Point） 可以通过如下的迭代序列找到：

\[ f(\top), f(f(\top)), ..., f^{h + 1}(\top) \]

其中， \(h\) 是 \(L\) 的高度。

基于格的数据流分析框架¶

一个数据流分析框架(Data Flow Analysis Framework) \((D, L, F)\) 由以下3个部分组成：

\(D\) （Direction）：数据流的方向——正向或者逆向；
\(L\) （Lattice）：一个包含值集 \(V\) 的域（即 \(V\) 的幂集）的格以及一个交汇操作符（Meet Operator）或者联合操作符（Joint Operator）；
\(F\) （Function Family）：一个从 \(V\) 到 \(V\) 的转移函数族（Transfer Function Family）。

那么，对于整个CFG来说，数据流分析可以被视为在所有结点的格的积格上面迭代地应用转移函数和交汇/联合操作的过程。因为定义域是值集 \(V\) 的幂集，而幂集本身就是一个天然的全格，记为 \((L, \subseteq)\) 。

那么，对于整个CFG来说，数据流分析可以被视为在所有结点的格的积格上面迭代地应用转移函数和交汇/联合操作的过程，假设有 \(k\) 个结点，则迭代算法的每一次迭代可视为 \(F_{L^k \to L^k}\) 。其中 \(L^k\) 是一个全格。所以，我们只需要证明 \(F\) 是单调的，就可以回答最后三个问题：迭代算法一定会达到不动点，并且达到的是序最小的不动点（对于正向、可能性分析，逆向、必然性分析也是类似的），且可以在 \(O(kh)\) 内达到，其中 \(h\) 是定义域格的高度。

\(F\) 有两个部分组成，一个部分是状态转移方程 \(f_{L\to L}\) ，我们可以发现，定义可达性分析的状态转移方程是单调的，类似的，变量活性分析和可用表达式分析的状态转移方程都是单调的。在我们进行其他分析的时候，我们设计状态转移方程时，需要保证其单调性。也就是说，一个设计糟糕的状态转移方程可能是不单调的，从而导致我们的迭代算法无法终止，或者无法求出符合预期的结果。

其实 gen/kill 形式的状态转移方程一般都是单调的，因为它的输出状态不会收缩。

因此满足不动点定理的条件，我们的迭代算法一定会达到一个最好（可能性分析则是序最小，必然性分析则是序最大）的不动点。并且，从不动点定理的证明中我们可以发现，迭代次数最多为格的高度，我们不妨记定义域格的高度为 \(h\) ，则每次迭代的最坏情况是 \(k\) 个格中只有一个格变化了一次，并且直到 \(\top\) 才找到不动点，在这种最坏情况下，迭代的次数为 \(k \cdot h + 1\) ，最后一次用于确认所有的数据流值都不会发生变化了。于是，我们便可以分析出算法的复杂度了。

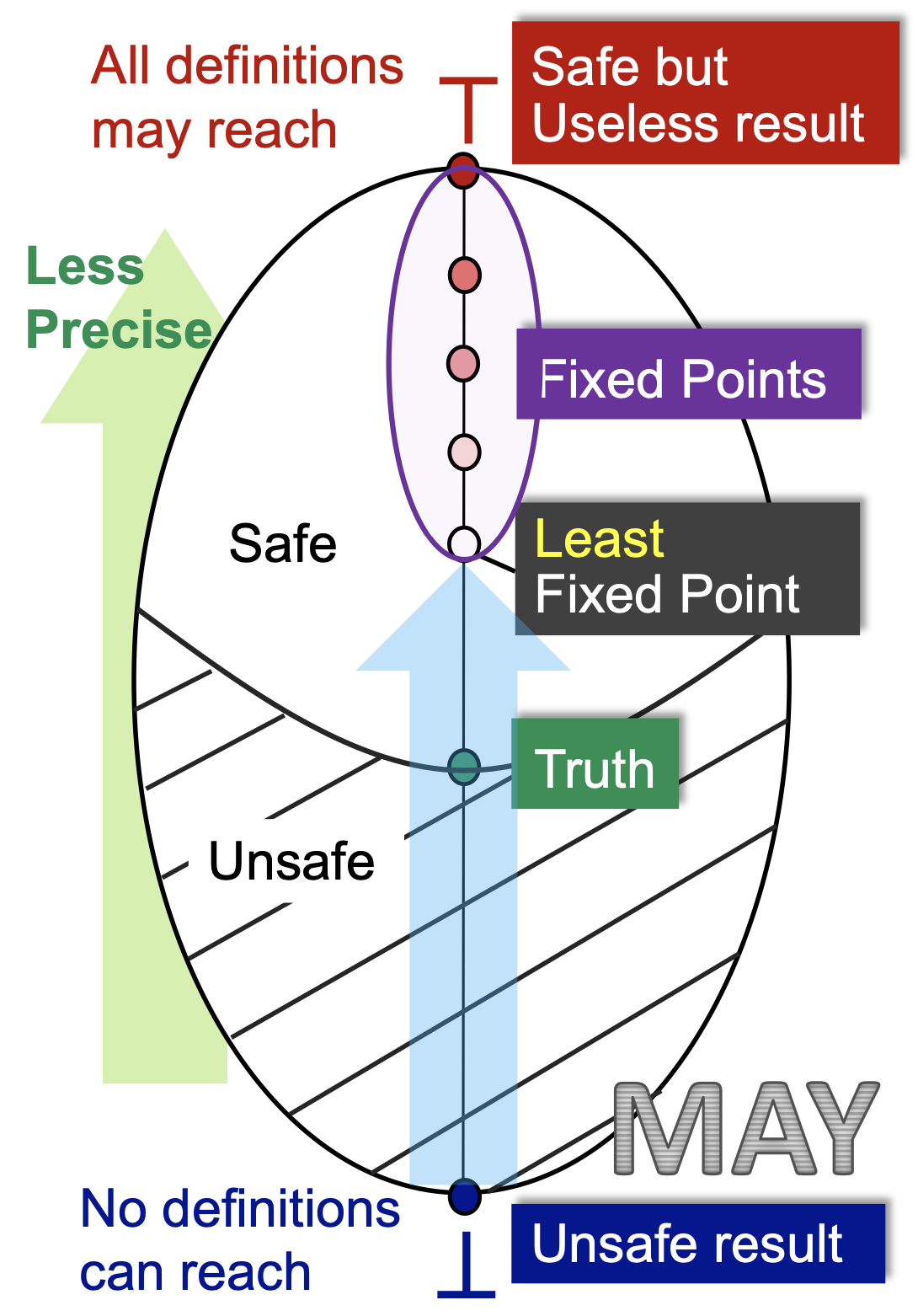
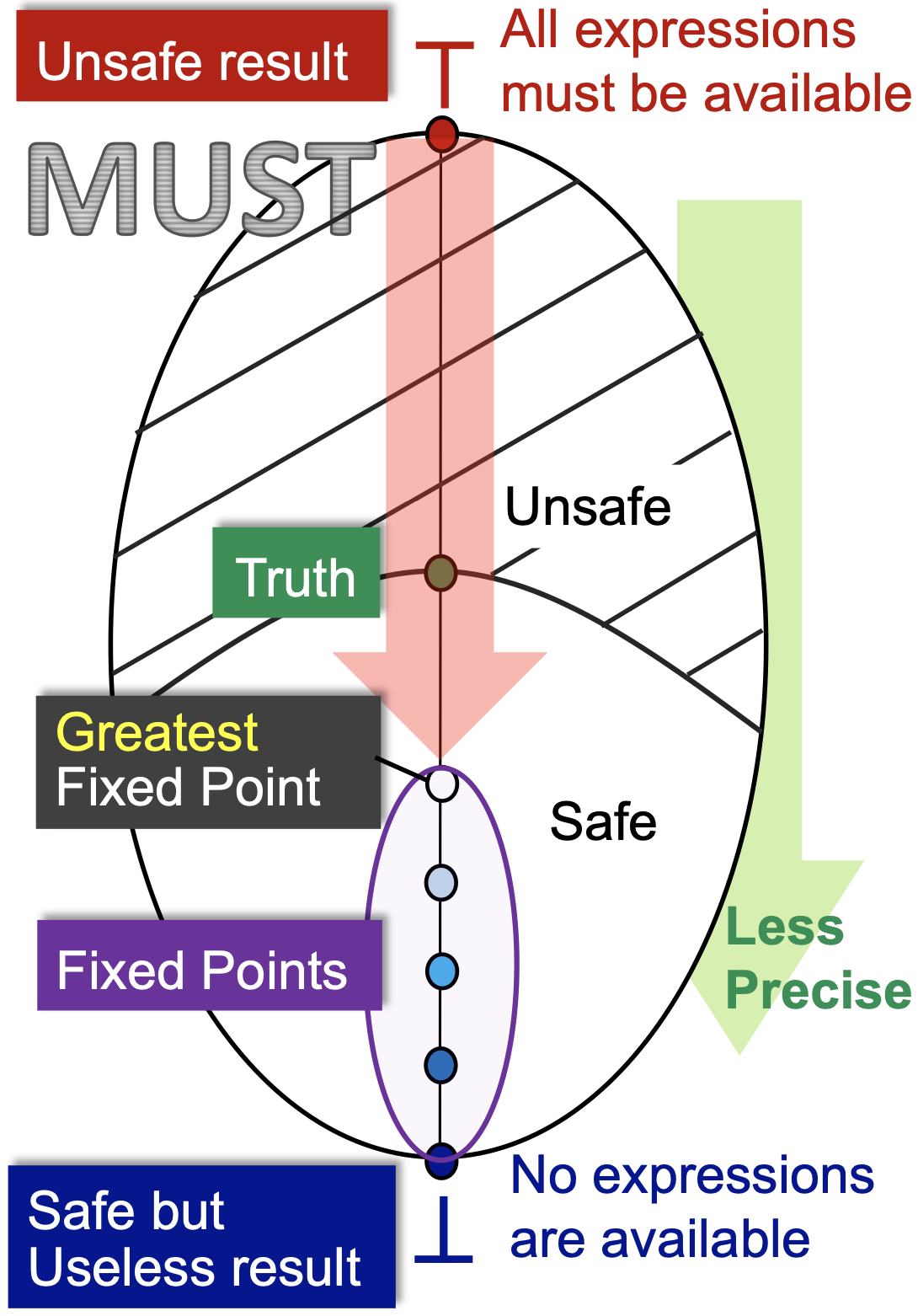
格视角下的可能性分析与必然性分析¶

三、指针分析与应用¶

TODO

四、技术拓展¶